
The example below will contain linear, quadratic and constant "pieces". In this other multiple functions are used to apply on specific intervals of. Due to this diversity, there is no " parent function" for piecewise defined functions. A piecewise function is a function, which is defined by various multiple functions. Their "pieces" may be all linear, or a combination of functional forms (such as constant, linear, quadratic, cubic, square root, cube root, exponential, etc.). They are also at the core of many computational methods. Evaluating a piecewise function only has one extra step when compared to a regular function, which is to determine which region we are in. Piecewise defined functions can take on a variety of forms. Piecewise functions appear in systems where there is discrete switching between different domains.
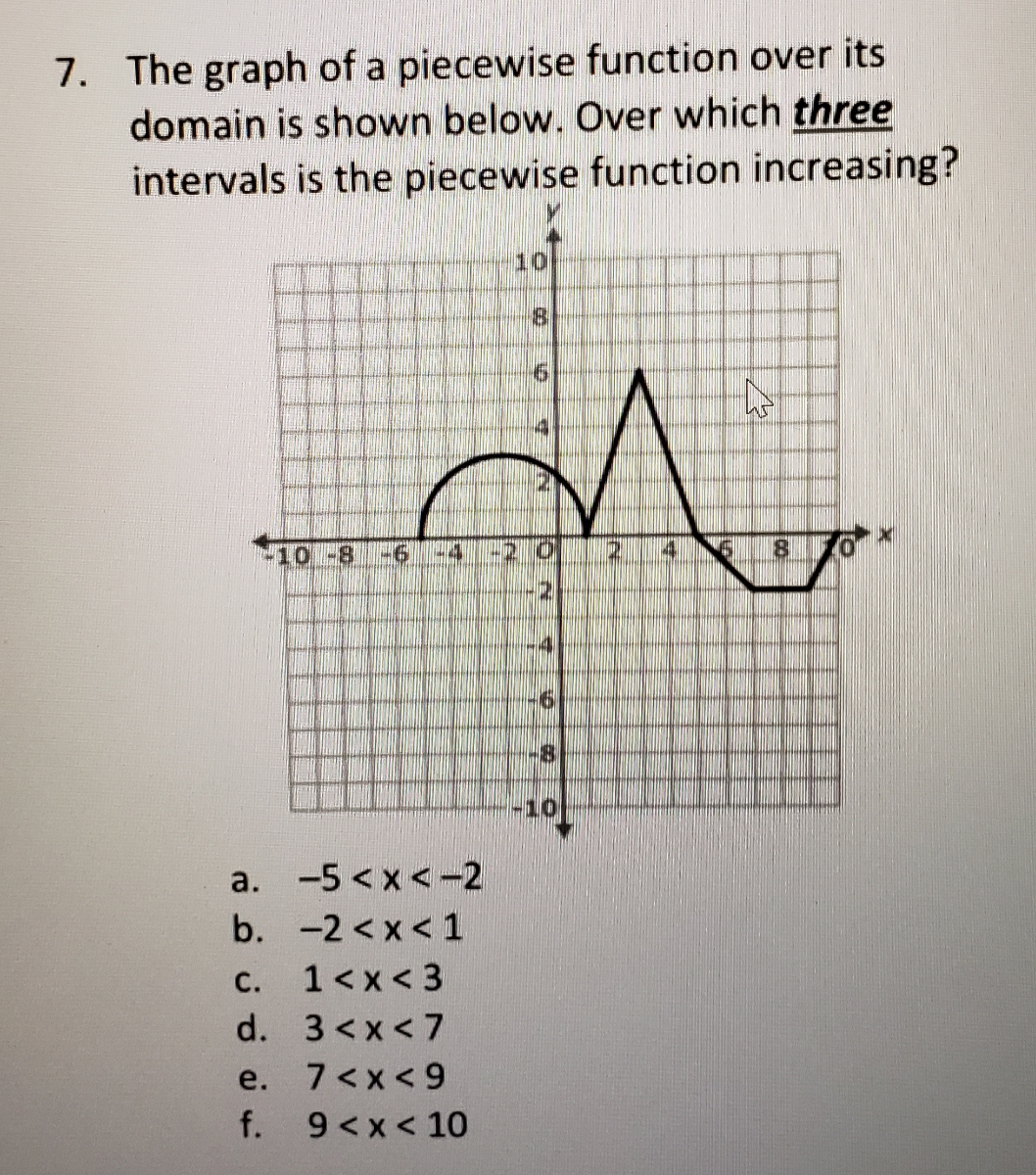
Because these graphs tend to look like "pieces" glued together to form a graph, they are referred to as " piecewise" functions ( piecewise defined functions), or " split-definition" functions.Ī piecewise defined function is a function defined by at least two equations ("pieces"), each of which applies to a different part of the domain. These graphs may be continuous, or they may contain "breaks". Consider the piecewise function defined by: f(x) 2x for x > 0 f(x) -x 2 for x < 0 You can see the graph of this. Example 1: A Piecewise Function That Is One-To-One. To find out if a piecewise function is one to one, we would apply the horizontal line test to its graph.

Note: Piece wise functions are little pieces of. Piecewise functions can be one to one, but not all of them are.
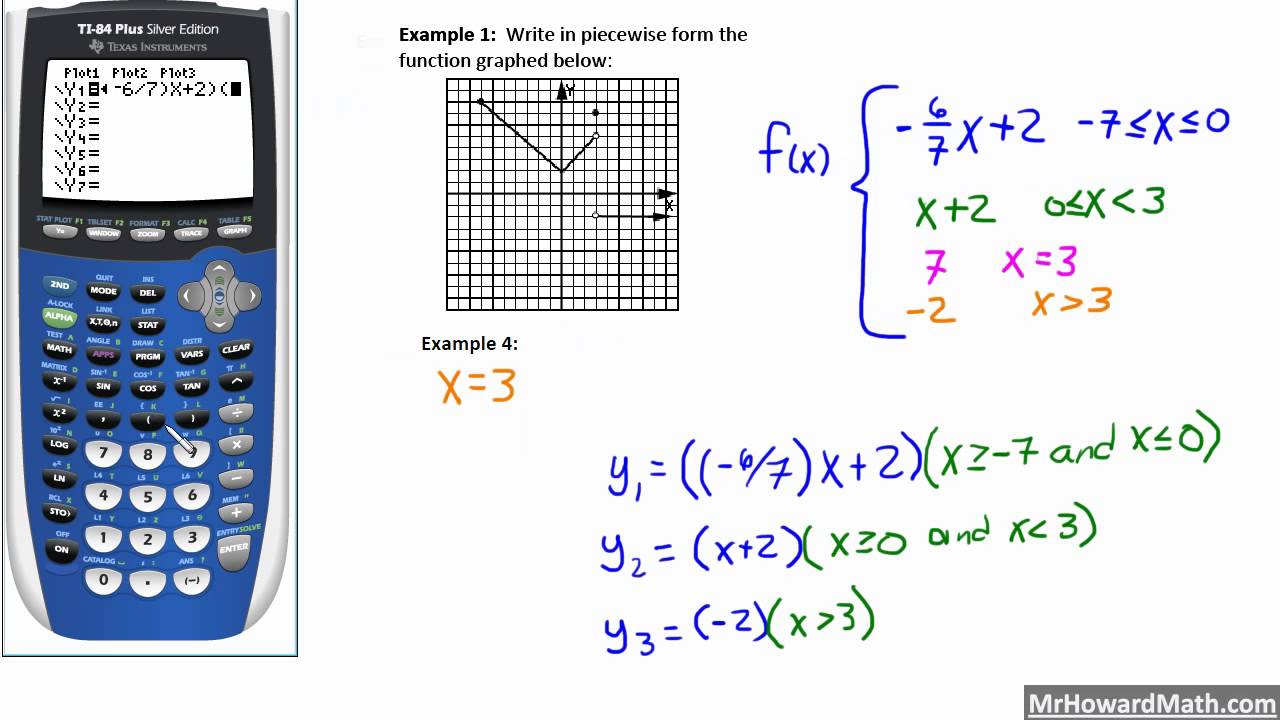
There are also graphs that are defined by "different equations" over different sections of the graphs. Select GRAPH mode from the main menu by using the arrow keys to highlight the GRAPH icon or pressing 5. We have also seen the " discrete" functions which are comprised of separate unconnected "points". We have seen many graphs that are expressed as single equations and are continuous over a domain of the Real numbers.


 0 kommentar(er)
0 kommentar(er)
